УДК 626.422.4

ФОРМУВАННЯ ТЕХНОЛОГІЧНИХ ПОНЯТЬ У СТУДЕНТІВ ІНЖЕНЕРНО-ПЕДАГОГІЧНИХ ФАКУЛЬТЕТІВ У ПРОЦЕСІ ВИВЧЕННЯ КУРСУ «ОСНОВИ ТЕХНОЛОГІЙ»

І. Й. Бочар, І. В. Гевко,

Тернопільський національний педагогічний університет (м. Тернопіль)

Постановка проблеми. Формування в майбутніх випускників інженерно-педагогічних факультетів технологічного мислення, уміння розробляти, проектувати та розраховувати технологічний процес виготовлення деталей і виробів вимагає стандарт освітньої галузі «Технології» [1, 48].

Вдосконалення навчального процесу на інженерно-педагогічних факультетах університетів, що передбачено у Наказі Міністерства освіти і науки України «Про порядок розробки складових нормативного та навчально-методичного забезпечення фахівців із вищою освітою» вимагає [2, 125]:

супроводження методичними засобами у вигляді конструкторсько-технологічних завдань усіх етапів технологічної освіти;

оволодіння системою технологічного мислення.

Згідно таких вимог актуальною є проблема формування технологічних понять у студентів інженерно-педагогічних факультетів у процесі вивчення курсу «Основи технологій». Для студентів розроблено й запропоновано алгоритм вибору прокатування гвинтових стрічок, методику проведення розрахунків ступеней закручування стрічок з різними профілями.

Мета статті – розкрити особливості формування у студентів інженерно-педагогічних факультетів технологічних понять для проведення вибору і розрахунків прокатування гвинтових стрічок під час вивчення курсу «Основи технологій».

Виклад основного матеріалу. Прокатування спіралей відрізняється рядом особливостей і, головним чином, асиметричним розподілом обтискання по ширині смуги. Внаслідок цього при проходженні смугової стрічки металу перерізом B*H0 через валки, поверхні яких утворюють трапецієвидну щілину, вона закручується у плоский виток ( спіраль з кроком T→H0 ) шириною В1=В+∆В, товщиною по внутрішньому краю H, по зовнішньому h.

Стрічка обкатується по всій ширині, і її товщина змінюється від Н до h за певним законом hy=f(y), де f(у) – спадаюча невипукла функція. Залежно від виду функції f(у), тобто від профілю гвинтової стрічки, процес закручування буде відбуватися з різною інтенсивністю, що викликає різницю в обтисканні зовнішнього краю при досягненні заданих параметрів [3, 110].

Наприклад, при прокатуванні спіралі по трапецієвидному профілю (рис. 1, а) буде відбуватися значне обтискання стрічки по зовнішньому діаметру. Збільшити товщину зовнішнього краю, зберігаючи незмінними параметри гвинтової стрічки, можна шляхом вибору оптимального профілю прокатки.

Рис. 1. Схеми профілів спіралей, які виготовляються холодним прокатуванням.

Відомі шляхи зменшення відносно обтискання, при яких частина ширини стрічки від внутрішнього краю не прокатується, а обкатування другої частини здійснюється або за лінійним законом, або за законом, коли на початку зони обкатування існує різка зміна відносного обтискання [4, 6]. На рис. 1 вони відповідають позиціям б і г. Значні внутрішні напруження, що виникають при цьому, несприятливо впливають на довговічність вибору.

Зменшити внутрішні напруження можна, вибравши профіль поперечного перерізу з гіперболічною твірною, при якій видовження кожної елементарної смуги металу пропорційне радіусу кривизни (рис. 1, д).

Закон зміни товщини гвинтової стрічки для такого профілю має вигляд:

(1)

,

де ŋ — коефіцієнт обтискання, ŋ=H/h.

Для спрощення виготовлення валків гіперболічний профіль можна замінити максимально наближеним до нього профілем твірна якого складається із ламаної лінії, місце і характер зламів якої розраховується із умови мінімально можливого поперечного переміщення металу при формоутворенні.

Якщо твірна складається із двох прямолінійних складових (варіант в), місце її зламу відступає від внутрішнього краю на віддалі b=B/(ŋ+1), причому товщина смуги в місці зламу:

(2)

.

Товщина зовнішньої кромки спіралей з гіперболічним чи наближеним до нього профілем більша, ніж в аналогічних спіралях з виконанням по варіанту а чи б (рис. 1).

Відомо, що з плоского кільця шириною В і внутрішнім радіусом r можна розгином отримати множину спіралей, пов'язаних з параметрами кільця відношенням:

(3)

.

Отже, при прокатуванні спіралей для порівняння ступеня закручування стрічок з різними профілями будемо використовувати значення внутрішнього радіуса прокатуваного кільця.

Розглянемо спочатку варіанти а, b, g, коли деформується весь поперечний переріз стрічки. Нехай теоретичний закон зміни товщини перерізу від H до h заданий функцією hy=f(у).

У результаті пружного стиску металу валків і смуги, згину осі валків, впливу зовнішніх зон та інших факторів товщина спіралі фактично буде змінюватись за законом:

(4)

,

де a(у) – величина, що враховує відхилення форми профілю спіралі під впливом перелічених факторів.

Значення радіуса закручування плоского кільця можна знайти із умови рівності об'єму виділеної ділянки стрічки довжиною до і після прокатки dl1 що записується рівняннями:

(5)

(6)

;

,

де (β – коефіцієнт розширення металу при прокатці, β=B1/B; λB – відносна витяжка металу по внутрішньому краю, λB=dlB/dl0; dφ – елементарний кут, на який відбудеться закручування стрічки елементарною довжиною dl0.

(7)

.

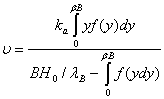Із умови де ka – коефіцієнт, що враховує відхилення спіралі від теоретичної форми, ka≈1.

Для варіантів прокатування спіралей (рис. 1, б, г), коли певна частина смуги обтисканню не підлягає, тобто при 0≤у<а, hy=H0 при у≥а; h=f(у), причому f(а)=H0; f(βB)=h – радіус закручення плоского кільця визначаємо із залежності:

(8)

,

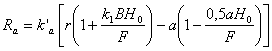де r – внутрішній радіус тільки обкатуваної частини стрічки, розрахований з умови відсутності необкатуваної, тобто із залежності (7); ka' – коефіцієнт впливу некатаної зони на відхилення профілю спіралі від заданої форми; ki – коефіцієнт, що враховує відношення жорсткостей прокатаної та непрокатаної частини.

Вказані залежності дають змогу розрахунковим шляхом встановити необхідні параметри прокатування: величину обтискання, оптимальний профіль і т. п.

Значення коефіцієнтів ka, ka', λ для сталей, які використовуються при виготовленні спіралей, і для розглянутих профілів при порівняно незначних обтисканнях близькі до одиниці. Ці коефіцієнти між собою не пов'язані, і їх можна легко визначити за один-два пробних проходи. Підналагоджування стану з урахуванням вказаних коефіцієнтів незначне і не вимагає перерахунку потрібного обладнання. Коефіцієнт ki визначається експериментально. Якщо прокатувати смугу з різким переходом від вільної частини до обтиснутої, наприклад, при незначній ділянці b (рис. 1, г), то прокатувана частина смуги видовжується по всій ширині, а некатана зона гальмує внутрішній край та інтенсифікує процес закручення смуги. При цьому коефіцієнти ka, λb, ki змінюються в широкому діапазоні і можуть бути визначені з належною точністю тільки шляхом експерименту.

Для випадку, коли прокатування здійснюється по трапецієвидному профілю, радіус закручування плоского кільця і коефіцієнт нерівномірності витяжки (рис. 1, а):

(9)

,

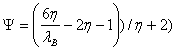де λB=1.

Для випадку прокатування по гіперболічному профілю:

(10)

.

Якщо прокатування по гіперболічному профілю (рис. 1, д) здійснюється без розширення (β=1), наприклад, в закритих калібрах, то залежності (10) набудуть вигляду:

(12)

; (11)     .

На виході смуги з валків вплив зовнішніх зон спричиняє значні напруження, значення яких залежить від прокатуваного профілю. Так, для спіралей з трапецієвидним профілем вказані напруження досить значні. Ще вищі вони для спіралей, прокатаних з необкатаною зоною. При прокатці по гіперболічному профілю вказані напруження визначаються тільки наявністю зони розширення.

Від напружень, що діють на виході смуги, практично залежить і звуження спіралі по внутрішній частині.

Для трапецієвидного профілю при прокатуванні плоского витка кільця без механізму проводки стискання волокон по внутрішньому краю залежно від величини обтискання становить λB=0,9-0,97.

За наявності вивідного механізму, який формує крок спіралі, процес формоутворення гвинтової поверхні значно ускладнюється. У такому випадку сили від розгину спіралі на крок можуть спричинити значний перерозподіл контактних напружень в зоні пластичної деформації, внаслідок чого спостерігаються значні (до 10%) відмінності коефіцієнтів нерівномірності витяжок при прокатуванні відповідно плоского витка і гвинтової поверхні в однакових калібрах. Так, при прокатуванні по трапецієвидному профілю видовження внутрішніх волокон при розгині на крок компенсує їх стискання при прокатуванні в плоский виток, і довжина внутрішніх волокон спіралі практично відповідає їх початковій довжині.

ВИСНОВКИ

Отже, вміння практично використовувати алгоритм вибору прокатування гвинтових стрічок і методику проведення розрахунків ступеней закручування стрічок з різними профілями передбачає необхідність оволодіння знаннями з математики, креслення, машинознавства та багатьох технічних дисциплін, розвиває у студентів інженерно-педагогічних факультетів творчий пошук, системне мислення та формування основ технологічних понять.

ЛІТЕРАТУРА

1. Бочар І. Й. Формування практичних умінь студентів інженерно-педагогічних факультетів під час розрахунків посадок підшипників кочення / І. Й. Бочар, І. В. Гевко. – Молодь і ринок. – 2010. – № 5 (64). – С. 48 – 52.

2. Бочар І. Й. Особливості проектування одиничних технологічних процесів механічної обробки студентами інженерно-педагогічних факультетів / І. Й. Бочар, Р. М. Горбатюк. – Наукові записки. – Серія: Педагогіка ТНПУ ім.В. Гнатюка. – 2006. – № 7.– С. 125 – 131.

3. Гевко Б. М. Механізми з гвинтовими пристроями / Б. М. Гевко, М. Т. Данильченко. – Львів: Світ. – 1993. – 208 с.

4. Шифрин Д. Я. Холодная вальцовка спиралей шнеков для самоходного кормоуборочного комбайна КСК-100 / Д. Я. Шифрин, В. Е. Гурвич, С. Н. Нудель. – Кузнечно-штамповочное производство. – 1984. – № 4.– С. 4 – 6.